昨天帶大家認識了Math.clz32()，最後還實作了fastLog2()，不知道各位是不是對log充滿著許多疑惑的XDD

沒關係，我都知道，還不需要敲碗我就直接端上桌給大家品嚐一下log吧！

熟悉的詠唱環節：

「寐偲，露個，炭！！！」

數學課

那我們就先來聊聊對數吧！

先來看看對數的長相：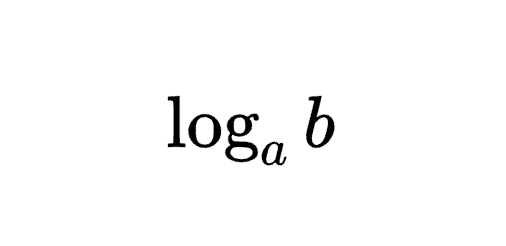

這樣的形式我們會用「log以a為底b的對數」來描述他，他的意思就是我們有兩個數a跟b，結果會是去計算a的多少次方等於b。

舉例來說，log以2為底8的對數會是多少呢？因為8會是2的三次方，所以我們會得到結果是3。

那為什麼要發明對數呢？

在數學上對數有很強大的意義，他可以讓數字達到簡化的效果，且取對數後能進行更簡易的計算，在數學上是一個很重要的存在。

• log(a * b) = log(a) + log(b)
• log(a / b) = log(a) - log(b)
• log(a^b) = b * log(a)

懂了對數大概的意義後就回到主軸吧～

Math.log10()

認識log之後Math.log10()就沒什麼問題了吧！看到函式名稱有個10應該就不難知道這是以以10為底的對數。

語法

Math.log10(x)

參數

傳入一個大於等於0的數字。

回傳值

他將會回傳以10為底x的對數。

但如果x小於0，將會回傳NaN。
（只有虛數的次方會是負數，通常這邊我們不會去討論虛數）

規範

那因為寐偲眾多的log咒語規範都大同小異，我們就統一在這簡單帶過，然後稍微看看有哪些地方不一樣吧！

恩...轉成數字...判斷NaN或正無限大...如果是1就回傳0...
喔！看到了如果是0就回傳負無限大！

這是什麼意思呢？？？等等回來討論，先繼續把剩下看完

如果小於0就回傳NaN...最後回傳以10為底的對數的近似值。

OK！沒什麼特別的了！

回到剛剛的疑惑吧！

我們要理解為什麼0的對數結果是負無限大之前我們先來理解負數次放究竟是什麼意思吧。

負數次方？

根據指數的定義，我們如果一個數a^(-b)，那得到的值就會是1 / a^b，可以觀察到如果指數是負數，那結果就會是取正次方的倒數：2^(-2)就會是1 / 2^2。

輸入0回傳負無限大

所以回到上面，如果要取0的對數，我們就要思考10的幾次方會是0，如果10^(-2)是1 / 100，10^(-3)是1 / 1000，到這邊應該就可以觀察到了吧！指數越小（往負方向），最後的結果就越趨近於0，所以我們就可以知道10的負無限大次方會非常接近0。

Math.log2()規範

只是把10換成2麻！輕鬆輕鬆～

Math.log()規範

咦？？等等，在數學中，我們通常會將log以10為底的10省略，所以log(10)就會是以10為底10的對數，但剛剛以已經有了Math.log10()，這個Math.log()又是什麼呢？

只是把10換成natural麻！輕鬆輕鬆～恩？等等

什麼是natural logarithm？？？

關於這個呢...

「我們以後將會專門做一期視頻為大家講解。」

Math.log1p()規範

這個一樣牽扯到了natural，先同上XDD

最後就來試用看看各種log吧！

console.log(Math.log() === Math.log10()); //false
console.log(Math.log10(10)); //1
console.log(Math.log10(1000)); //3

console.log(Math.log2(2)); //1
console.log(Math.log2(16)); //4
console.log(Math.log2(32)); //5
console.log(Math.log2(4)); //2
console.log(Math.log2(1)); //0

console.log(Math.log(Math.E)); //1  ???????

console.log(Math.log10(1)); //0
console.log(Math.log2(1)); //0
console.log(Math.log(1)); //0

console.log(Math.log10(0)); //-Infinity
console.log(Math.log2(0)); //-Infinity
console.log(Math.log(0)); //-Infinity
console.log(Math.log1p(0)); //-Infinity

參考資料：
維基百科-對數
中央大學數學系專題-指數與指數函數
ECMAScript-Math.log10()
ECMAScript-Math.log2()
ECMAScript-Math.log
ECMAScript-Math.log1p